


|

|
|
|
Методы решения
тригонометрических уравнений
1.
Решение
простейших тригонометрических уравнений
2.
Решение
тригонометрических уравнений разложением на множители
3.
Решение
тригонометрических уравнений сводящихся к квадратным уравнениям
4.
Решение
тригонометрических уравнений преобразованием суммы тригонометрических функций в
произведение
5.
Решение
тригонометрических уравнений преобразованием произведения тригонометрических
функций в сумму
6.
Решение
тригонометрических уравнений с применением формул понижения степени
7.
Решение
тригонометрических уравнений как однородное
8.
Решение
тригонометрических уравнений с помощью введения вспомогательного аргумента
9.
Решение
тригонометрических уравнений с помощью универсальной тригонометрической подстановки
10.
Решение
тригонометрических уравнений с помощью замены неизвестного
11.
Решение
тригонометрических уравнений с помощью оценки левой и правой частей уравнения
(метод оценок)
12.
Решение
тригонометрических уравнений содержащих тригонометрические функции под знаком
радикала
1.
Решение простейших тригонометрических уравнений
![]()
![]()
![]()
По определению арифметического квадратного корня перейдем к равносильной системе уравнений.
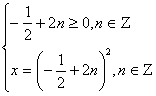
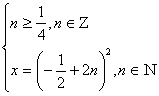
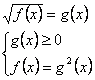
Ответ:![]()
2. Решение
тригонометрических уравнений разложением на множители
![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]() или
или ![]() решений
нет
решений
нет
![]()
![]()
Отметим полученные решения и область определения на тригонометрическом круге.

Решением уравнения является:
![]()
![]()
Ответ: ![]()
3. Решение тригонометрических
уравнений
сводящихся к квадратным уравнениям
![]()
![]()
![]()
![]()
Пусть ![]() , тогда
, тогда ![]()
![]()
![]()
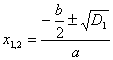
![]()
![]() или
или ![]()
![]() Т.к.
Т.к.
![]()
![]() при
при ![]() , то корней нет.
, то корней нет.
Ответ: ![]()
4. Решение
тригонометрических уравнений преобразованием
суммы тригонометрических функций в произведение
![]()
![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: ![]() ;
;![]()
![]()
5. Решение
тригонометрических уравнений преобразованием
произведения тригонометрических функций в сумму
![]()
а) Найдем область определения функции.
![]()


![]()
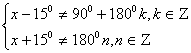
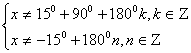
Областью определения данного уравнения является:
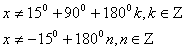
б) Решим данное уравнение.
![]()
![]()
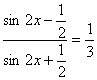
![]()
![]()
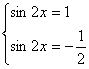
![]()

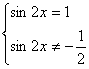
![]()
![]()
![]()
Ответ: ![]()
6. Решение
тригонометрических уравнений с
применением формул понижения степени
![]()
![]()
![]()
![]()
![]()
![]()
Пусть ![]() , тогда
, тогда
![]()
![]()
![]()
![]() или
или ![]()
![]() Т.к.
Т.к.
![]()
![]() при
при ![]() , то корней нет.
, то корней нет.
Ответ: ![]()
7. Решение
тригонометрических уравнений как однородное
Однородное уравнение – это уравнение, в котором каждое слагаемое имеет одну и туже степень.
![]() , где
, где
![]() - действительные числа.
- действительные числа. ![]() - показатель
однородности.
- показатель
однородности.
![]()
![]()
![]()
![]()
Если ![]() , то и
, то и ![]() , что противоречит основному тригонометрическому тождеству,
значит
, что противоречит основному тригонометрическому тождеству,
значит ![]() . Разделим обе части на
. Разделим обе части на ![]() , получим
, получим
![]()
![]()
![]()
![]()
![]()
Ответ: ![]()
8. Решение
тригонометрических уравнений с помощью
введения вспомогательного аргумента
![]()
Т. к. ![]() , то корни есть.
, то корни есть.
Разделим обе части уравнения на ![]() , получим
, получим
![]()
Т. к. ![]() и
и ![]() , то существует такой угол
, то существует такой угол ![]() , что
, что ![]() , а
, а ![]() , тогда получим
, тогда получим
![]()
![]()
![]()
![]()
![]() Ответ:
Ответ:
![]()
Теория.
![]()
1) если ![]() , то уравнение однородное.
, то уравнение однородное.
2) если ![]() и
и ![]() (то есть хотя бы одно из чисел
(то есть хотя бы одно из чисел ![]() или
или ![]() не равно 0), то
разделим обе части уравнения на
не равно 0), то
разделим обе части уравнения на ![]() , получим
, получим
![]()
Т. к. 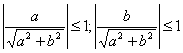 и
и 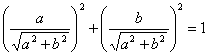 , то существует такой угол
, то существует такой угол ![]() , что
, что ![]() , тогда
, тогда
![]()
![]()
а) если,  т. е.
т. е. ![]() , то корней нет.
, то корней нет.
в) если, 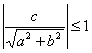 т. е.
т. е. ![]() , тогда
, тогда
![]()
![]()
![]()
Т. к. ![]() , то корней нет.
, то корней нет.
9. Решение
тригонометрических уравнений с помощью
универсальной тригонометрической подстановки
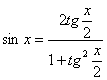
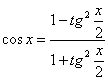
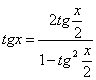
![]() (1)
(1)
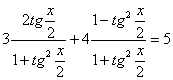 (2)
(2)
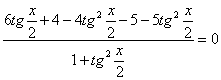
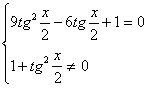
![]()
![]()
![]()
![]()
При переходе от уравнения (1) к
уравнению (2), могла произойти потеря корней, значит необходимо проверить, являются
ли корни уравнения ![]() корнями данного
уравнения.
корнями данного
уравнения.
![]()
![]()
![]()
Проверка.
Если ![]() , тогда
, тогда
![]()
![]() - не верно, значит
- не верно, значит ![]() , не является корнями исходного уравнения.
, не является корнями исходного уравнения.
Ответ: ![]()
10. Решение
тригонометрических уравнений
с помощью замены неизвестного
Уравнение вида ![]() решается следующей
заменой
решается следующей
заменой ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
Способ I
![]()
Пусть ![]() ,
, ![]() ,
, ![]() ,
, ![]() , получим
, получим
![]()
![]()
![]()
![]() или
или ![]()
![]()
![]() (3)
(3)
Разделим на ![]() , получим
, получим ![]()
![]()
![]()
![]() Т.
к.
Т.
к. ![]() , при
, при ![]() , то корней нет.
, то корней нет.
Ответ: ![]()
Теория.
![]() , при
, при ![]()
Доказательство:
![]()
Шесть способов решения уравнения (3).
1.
применение формулы ![]() .
.
2.
через ![]() .
.
3. привести к однородному уравнению второй степени.
4. способ введения вспомогательного аргумента.
5.
с помощью неравенства ![]() , при
, при ![]() .
.
6. метод оценки левой и правой частей уравнения.
![]()
Способ II
![]()
![]()
![]()
![]() или
или ![]()
Разделим на ![]() , получим
, получим ![]()
![]()
![]()
![]() Т.
к.
Т.
к. ![]() , при
, при ![]() , то корней нет.
, то корней нет.
Ответ: ![]()
11. Решение
тригонометрических уравнений с помощью оценки
левой и правой частей уравнения (метод оценок)
12. Решение
тригонометрических уравнений содержащих
тригонометрические функции под знаком радикала
Пример №1
![]()
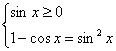
![]()
Решим уравнение 2.
![]()
![]()
![]()
![]()

![]() или
или ![]()
![]()
![]()
![]() Отметим поученные решения и
условие 1 на тригонометрическом круге.
Отметим поученные решения и
условие 1 на тригонометрическом круге.
Ответ: ![]() ,
, ![]()
Пример №2
![]()
![]()
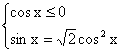
![]()
Решим уравнение 2.
![]()
![]()
Решим квадратное уравнение
относительно![]() .
.
![]() и
и ![]() то корней нет.
то корней нет.
Отметим поученные решения и условие 1 на тригонометрическом круге.

Ответ: ![]()
|
|